Toward the theory of Flying Wings
Translated from the German by Yoram Leshinski (Many thanks!)
Aerodynamics
From Lilienthal (1892) to Junkers (1910), the creation of lift was the leading thought that gave all constructs their form. Even the empennage should create lift. The making of airfoils for wings and empennage reflected the strong camber of a bird's airfoil, that Lilienthal had realized and measured as best for creating maximum lift.
The creation of lift was emphasized in 1852 through by Magnus. Magnus, who as an artillery officer studied the flight of rotating projectiles in crosswinds, gave the correct explanation for the projectiles missing the targets. Rotation and crosswind gave a force perpendicular to the flight direction: Lift. That phenomenon (known today as the Magnus effect) can be clearly observed on "cut" tennis balls or "sliced" golf balls. A cylinder revolving on its axis (with circular flow lines, whose speed is inversely proportional to the radius) will be brought into a parallel flow, so that the local speeds overlap. An asymmetric flow line is created in regards to the horizontal, that means lift, a symmetry remains in regard to the verticals, and so no resistance is created. If you envision the image distorted through a mathematical trick, then from the circle you will get the Joukowski Airfoil. This transformation is also easily achieved through drawing.
If you write the circulation 
then the lift is (discovered independently by Kutta and Joukowski): 
or when the stagnation pressure, 
is introduced and 
substituted with 
where 
with 
and 
.
The flow lines of the rotating cylinder in a parallel flow can be easily made visible through experiments in a hydrodynamic tank., If instead of a rotating cylinder, a cambered plate is submerged in the water flow, then the picture of the flow lines, a little bit further from the cylinder or the plate, remains unchanged. because of symmetry principles around the vertical, the lift can be viewed as an effect on the cylinder axis and also on the middle of a cambered plate, that is 50 % of the airfoil. The lift is then present, even so the AOA is zero, its coefficient stated as clo. The circulation belonging to each cambering resulting through this, that the down flow direction at the trailing edge, in cylinder and plate, must be the same. You can make it visible, with the same experiment configuration, that a flat plate, or even better, one with a symmetrical airfoil enveloping it, will create the same flow line image (this will always take place when the lines are viewed a little bit further out from the cylinder area and the down flow angle is now through the given angle of the flat plate).
Anchor on the spot of the cylinder axis the point of 0.25 t (t = airfoil length) of the turnable symmetrical airfoil, and you will also see that no moment is created, and it can be perceived that the lift affects at t / 4. This occur in all AOA, as long as the flow does not become turbulent and detaches. In t/4 point the moment does not change when the AOA changes (i.e. moment = zero). Therefore, you call that point the Neutral Point of the airfoil. Also in the previous example, you can give the cambered plate, enveloped with a symmetrical airfoil, an extra AOA, through which the down flow direction and with it the circulation, and with it the lift, will be increased. At the same time, the neutral point remains inside t/4, yet a moment exists in all AOA, cmo = cao * t/4, in which t/4 of the leverage arm of the zero lift in t/2 indicates to the neutral point 0.25 t. In other cambered airfoil centre lines, cmo must be calculated or in wind tunnel measured. If you bend the centre line in the front (at the airfoil nose), the cao will be raised, cmo stays small. If you bend the centre line in the back, cao is raised together with cmo. Through combination this brings you to a S-form centre line, where cmo = 0 and through this, a "fixed pressure point" airfoil can be constructed.
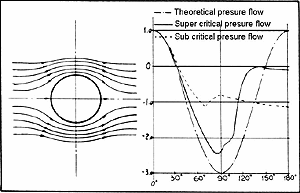
With that, the lift and the moment in two-dimensional flow are explained, but a resistant is not yet evident. As said in the first chapter, Prandtl explained this from the friction, which develops on the top surface of a flow-surrounded body, and is therefore called friction resistance. The flow pattern of the motionless cylinder in the parallel stream is experimentally difficult to show, as the friction on the top surface of the local speeds changes opposite the theoretical, whereby the pressure distribution shifts and, finally, even the separation of the stream follows. Friction resistance to the cylinder top surface and the friction of the air layers between the streamlines changes the picture behind the body (the symmetry is disturbed), and thereby causes air resistance. On the front side of the cylinder is the additional flow pressure Dp = q in the center. The flow pressure is reduced on both sides to zero when the cylinder is raised up to the angle of 30 degrees, thus the local velocity is that of the free unimpaired flow. According to the Bernoulli law, the pressure reduces itself up to a cylinder angle of 90 degrees, since the speed rises. The pressure field on the front of the cylinder can be divided into its components in the direction of the flow, which results, between the cylinder angle 0 to 30 degrees in pressure components to the rear, and from 30 to 90 degrees in suction component to the front. Both eliminate themselves perfectly, so that half of the cylinder experiences no pressure resistant between 0 and ±90 degrees.
|
The mach number, the relation of flight speed to the speed of sound, was stated with the resistant estimation. If one imagines the front-projecting
surface multiplied by the rate of v of the flight, then one receives a volume which, per second from the front to the rear, must be led past the airplane. This occurs, as is very well visible on the cylinder in the hydrodynamic tank,
at high speeds near the largest cross-section. There will be, as stated above, no extra resistance added to the friction. If you think of the air as compressible (as is necessary at high speeds), then the volume to be
transported is multiplied by the density V and you receive mass. The transportation of that air mass past the airplane (from the front to the rear) is therefore different from the "volume transport". In the place of the highest
velocity (connected with the biggest negative pressure by the Bernoulli equation), the negative pressure now also changes the density
(reduced), so that, in order to transport the mass of air, high speeds must again now be increased. The product V * v now becomes instrumental, and we have to examine if it has a maximum (whether there is a speed at which 
. At a higher speed the density
decline will be larger, since it corresponds with the speed increase and, with that, less air mass flows laterally by the airplane. It is easily
derived that the maximum existed and the appropriate speed is that of the sound. This locally occurring speed of sound, at further
increase of the flight speed, makes the continuity of the flow not possible. Therefore the flight mach number, at which locally the speed
of sound occurs, is called critical and the speed range beginning with it transonic (to approximately mach number 1.3). At Mach 1.3,
purely supersonic flow begins. The transonic stream is still today in a research status. On the other hand, the supersonic flow is easy to calculate.
The airplane's volume distribution perpendicular to the flight direction (as found in a thick wing, patented by Junkers), loses its physical
foundation with the critical mach number. However, this is shifted by the sweep of the wing to higher values, up to approximately M = 0
.9. In the supersonic range different laws apply, since air is compressed, which leads to energy loss. Here the Junkers patent cannot be
applied any longer. Furthermore, it is practical to keep the front-projecting surface small, that is, to lay out the space in longitudinal
direction. After a suggestion from H. Multhopp (to me in 1955), it is best to calculate the cross-sections of the airplane as 
at M = 1. The factor "cte" is obtained from the desired airplane volume, the largest cross-section area smax.
(surface) in 50% of the total length of the airplane. X in the above equation is set from -1 to +1. The shift of the critical mach number by the sweep-angle follows only approximately the factor 
, where as the sweep-angle refers to the minimum airfoil pressure, as is
physically necessary. The influence of the wing-tapering on the shifting of the critical mach number is not yet investigated, but is, with an
increase of the tapering, to be expected, which is especially prominent in the delta wing. A thickening of the wing around 1% diminishes
the critical mach number around approximately 1.5 %. One may conclude from this that the sweep is more effective.
For the performance calculation in the transonic flight it make sense to set the thrust in relationship to the front-projecting surface and so to define a calibrated load. The thrust at travel height and the number of revolutions of the engines at travel speed are to be considered. The thrust must be divided by smax. and one receives so the dimension daN / m2. The calibrated load and the space distribution according to the Multhopp equation is, with that, opposed to the Junkers patent and banishes the wing only airplane into the subsonic flying range. The tail-less airplane however, which represents only a partial solution in the subsonic to the wing-only airplane, is, in the transonic or supersonic, a must for flight performance and safe controllability. The swept wing does not only shift the critical mach number to higher value. It diminishes the resistance jump near the speed of sound and reduces the lift collapse, that the strait wing suffers. That's why an airplane without sweep above the critical mach number (or close to M = 1) is uncontrollable. Since in supersonic flight the flow is two dimensional, the side proportion can be kept small. With strong sweep you get the delta airplane, which is controllable in the whole transonic area. The supersonic aircraft is therefore optimal with regards to the resistance and for safety reasons (controllability) a tail-less delta airplane. The wing thickness should be, as is static-constructive necessary, as small as possible. The fuselage must haven the volume for the fulfillment of the mission, preferably with round cross-section, in order to form a pressurized cabin, which is unavoidable with the travel heights in the stratosphere. Junkers could not possibly foresee this development of aviation 1910. It appeared only after the end of the war, 1945 and later, and can be seen in the construction examples of the "Mirages" and "Concorde", which represent optimal configuration. The tail-less airplane, which Junker did not patented and did not use in his projects J1000 and G 38, was now the best solution in the supersonic.
In the subsonic area however the tail-less airplane is a partial solution of the wing- only airplane and was probably understood as such, so that the flight characteristics and the controllability could be studied.
For performance comparison to the tail airplane the wing-only airplane is to be considered, as appropriate for the mission. The attempts of different designers with tail-less gliders and sail-planes in the twenties have so their justification, also then when the wing was connected with struts to the fuselage and thus happened what Junkers wanted to eliminate with his patent. The flight characteristics (particularly in stretched flight) where with these samples further developed. The strutted swept wing was also combined with tail airplanes (falcon, super-falcon), although the strut force component in the wing had to be led over diagonals and secondary spars, which generally are not intended for it. It is not to be said that the tail-less airplane is statically more difficult than a tail airplane, but only that the temporary solution with struts (in regards to the Junkers patent) had led to illogical systems and that the, by Junkers already 1917 constructed, cantilever wings meant a large step ahead in the direction of the wing-only airplane.
Lift distribution
Air resistance in the subsonic region, in which from now on the wing-only airplane is to be seen, was clarified by two messages in the Lifting Wing Theory by L Prandtl (published 1918). The diverted induced resistance becomes a minimum, if the lift is distributed over the span in the form of a half ellipse, in the case of a given span and a constant weight of the airplane. If now the wing has the form of an ellipse, then (without washout) the lift coefficient is same in every place of the span. Close to the max. lift a local flow separation can bring a rolling moment around the longitudinal axis of the airplane, which the pilot can barely adjust with the aileron, because the whole wing is close to the max. lift. The elliptical wing was therefore sparsely used for reasons of the flight characteristics and production. The wing tip (according to the suggestion of Ahlborn) was made thicker, similar to the Zanonia-Samen. Through that the local coefficient of lift at the wing tip is smaller than in the other places of the wing (even at elliptical lift distribution), so that a flow separation is not to be expected there. Tail-less airplanes, according to the Zanonia principle, can have elliptical lift distribution.
The lift was according to the mathematical derivative from the circulation of Kutta-Joukowski in wing span direction as constant,
because the created vortex could not change. L Prandtl explained, in July 1918 in Goettingen, that the above problem could not apply
in three dimensions, because the bent carrying vortex at the wing tip induced on the carrying line of the vortex center, in 1/4 of the depth
, a downward speed w. In the model of the "horseshoe vortex", w becomes infinite at the wing tips, which is physically impossible. Prandtl assembled therefore the carrying vortex 
from many single vortices, each resembling a horseshoe, and proofed: if 
varies the
intensity over the wing span (proportionally to an ellipse), then the down-wash w is constant over the wing span, the wing tip excluded.
He derived an equation, from which the induced down-wash can be calculated and from it the resistance, which was this way calculated
with the lift. The down-draft speed w of the vortex center multiplied by the lift, represents an energy per second, hence a performance,
that must be equivalent to another force times speed, therefore resistance times airspeed. The elliptical lift distribution with constant down-wash over the wing span or constant ai(induced AOA), resulted in a minimum for this "induced resistance". The equation from
Prandtl, in the meantime, can not generally be solved. At the wing tips, for which Prandtl had required that 
, the down-wash remains undetermined.
You could keep this zone small, point like, if 
, however, the down-wash at the wing tip was first ascertained when 
.
Two different lift distributions result from it, those with perpendicular tangent at the wing tip and those with horizontal tangent.
Consequently, different authors tried to describe the lift distribution precisely enough to be accepted by the scientist. Schrenk gave
1925 the simplest solution, to take the average value between the depth distribution and the equal area ellipse, which results in a good
approximation and is still completely sufficient today for the calculation of empenage loads. This approximation had to fail, if the wing
had a wash-out. Lippisch, in 1932, came up with an approximation method (Sport Flying 1932), in which the wash-out where included.
He also mentioned the lift distribution with zero-tangent at the wing tip, later termed by me (Horton) as bell distribution. In 1938 Multhopp succeeded to separate the critical wing tip and to give a solution to the equation for the determination of the lift distribution by linear equations at certain points of the wing span (Lufo 1938).
(These papers of Lippisch and Multhopp, as dissertation recognized, would have been enough to be received with honour in every university, however both were missing in the fulfillment of formalities of the curriculum, in order to receive acknowledgment.)
|
|
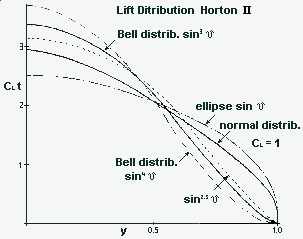
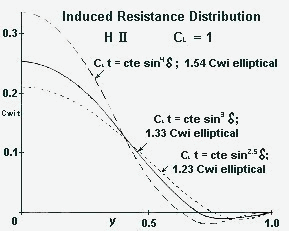
Fig. 2 Lift distribution along the wing span. With a central angle d , which indicates the coordinates from 00 to 1800 as Y = cos d in span direction, and which describes the elliptical lift distribution with cl t = c * * t * e * sin d , can also define the bell distribution with cl t = c * t * e sin3 d . In the case of a narrowing wing, in the example is the wing of the H II represented, you get without washout a "Normal Distribution", which has less lift at the wing tip than elliptical wing with the same area, however both distributions have much more lift there, than the stretched bell distribution. With tail-less airplanes, whose wing is arranged after the volume curve, the bell distribution is necessary, to prevent to high lift values at the wing tip. Since the distribution of sin2 d is theoretically not possible, was the H II after the c * t = c * t * e * sin3 d curve constructed, with which in Y = 1 a zero-tangent is available; contrary to the elliptical and normal distributions, with which at the wing tip a vertical tangent occurs. The distribution of sin4 d , that leads to larger induced resistance and those with sin2,5 d are also drawn in, since these have likewise zero-tangents, the curve sin2,5 d remained however only an attempt, because the flight characteristics worsened and a larger ability was required by the pilots being, even so the performance improved do to the smaller induced resistance. |
). With the designations of Multhopp is the bell distribution: cl* t = cte sin3d. Also was investigated cl * t = cte * sin4d and cl.t = sin2.5d,
as well as the normal distribution (without washout), and necessary washout and induced resistance distributions for cl = 1.
It results:
|
||||||||||||||||||||||||||||||||||||
Negative yaw meant that an aileron deflection produces a moment around the vertical axis opposing the turn, which must be balanced with the rudder.
|
|
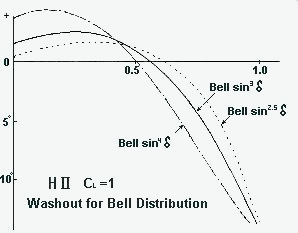
Fig. 3 The necessary washout (to give the H II the bell distribution) is recorded in the above graphs. It is understandable that with a cl total smaller than one, proportionally also the washout becomes smaller. The rudder kinetics has to adapt to the graph in such a manner that with the rudder deflection the washout graph is preserved for a modified cl total, thus with the rudder deflection a variable washout is arranged. |
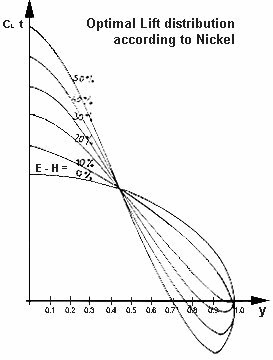
K. Nickel has, in 1848 (Tübingen Diss.), calculated Distributions, which resulted in a minimum of the induced resistance. Unfortunately without specifying the resistance distribution and without the data which are necessary for the application. The occupying authorities had forbidden the aviation research at that time. It would be to be welcomed, if today the work were concluded. In the distributions of Nickel is the vertical tangent Y = 1 allowed, so that quite different lift distributions develop than those for the bell form. A graph, which Dr. Karl Nickel gave the author (Horton) in Argentina, is shown. (Fig. 6)
|
|
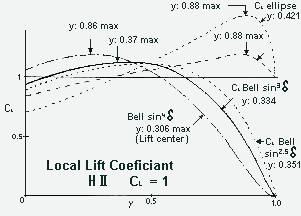
Fig. 4 Local lift coefficient at different lift distributions calculated for the wing of the H II at cl-total = 1.0. Y indicates the center of lift in span direction. Close to it should, with increase of the AOA, the separation the flow of take place first, so that from the locally decreased lift no moment will occur. The center of lift and the CG of the airplane must correspond in x-direction, if at the whole wing cm0 = 0 and no rudder deflections exist. The elliptical lift distribution has its max. cl with Y = 0.88, their center with Y = 0,421, therefore it is quite unsuitable for this wing shape. The bell distribution with the max. lift coefficient in Y = 0,37 and center of lift in 0.33 fulfills quite well this condition (small differences are controllable), if the wing tips with their rudders operate in strong flow. The wing tip must be well protected against flow separation, which the bell distribution ensures at all tapers, up to the triangle wing. |
Because of the, towards the wing tip, diminishing lift, the reduced lifting vortex trails off in single vortices in flight direction to the rear. These induce a down wash at the place of the main vortex according to the Pradtl's lifting wing theory. In the case of a swept wing the segments differ from those of the strait wing, so that with it shifts occur and the wing tips receive less down wash. In addition, the lifting single vortices influence each other at the sweep bend (that is right and left), and there, through the local
|
|
Fig. 5 The induced resistance distributions of all bell distributions show propulsion at the wing tip. This is favorable with aileron deflection, since the Yaw changes its value around the vertical axis, thus becomes positive. If the rudder kinetics preserves the bell distribution at all cl-value, then the Yaw is avoided, or even positive, at all cl-value. This is, on the one hand, favored by the pilot, on the other hand a large part of the rudder effect is thereby superfluous |
If the lift distribution has a turning point (as with the bell distribution), the vortices going off to the rear
|
|
Fig. 6 Optimal lift distribution according to K. Nickel. At a given lift and longitudinal force the induced resistance is minimal |
|
|
Fig. 7 With the "Robot", installedat the wing tip of the H II , Wool tuffs could be photographed, which displayed the flow direction there. With bell distribution and local cl = 0 a vortex is not available there, the direction of flow on top and bottom side are the same. (The sheet metal at the other wing tip serves for the moment balance around the vertical axis. The asymmetry is caused by the tubing and the Camera.) Wool-tufts on the white-painted wing root were likewise photographed, in order to make the center effect visible. This however was without success, since the current always fitted and so it could be proven that the center effect results from the ai -distribution and not by a separation of the flow. |
Flaps
Junkers built in 1925, for the first time on the T 29 airplane, landing flaps in form of an auxiliary wing, which divided, worked at the same time at the outer wing also as aileron. The max. lift coefficient almost doubled itself during optimal auxiliary wing position. With the same landing speed one could thus almost double the weight/sqf, or to build a wing only half as large with same flying weight. This Junkers double-wing, caused different landing flaps systems to be ignored, seemed to out-date the wing-only idea, because the wing could, and had to, become smaller. In addition it became obvious that the occurring pitch-moment needed an empennage for the balancing. It is therefore understandable that Junkers, after the G 38 (which also had these landing flaps), developed the tail ("normal") airplane Ju 52, in order to use the possibilities that his auxiliary wings invention brought. Today these double-wings are not used any more, although their advantages in relation to other systems continue to exist and the possibilities with Laminar airfoil were not yet sufficiently examined. Therefore, in the development of the wing-only, landing flap combinations had to be included, with which we dealt in the preceding sections.
It must be still pointed out however that the airfoils of the tail airplanes at that time with approximately circularly curved center line, after integration of the landing flaps (that caused the maximum lift for landing), were changed to airfoils with small airfoil moments, which are also suitable for tail-less airplanes.
A substantial feature in the difference of the wing shaping of both building methods was thereby omitted. Now it had to be proven that landing flaps are also useable with the only-wing. The DVL also announced a patent for a flap form, which produced no moment. However it was overseen that a lift increase at the wing root of the swept wing results in a backwards acting moment, that the airfoil moment of the flap is however top-heavy (thus opposite)had been ignored. There are possibilities, however, of combining the moments in such a way that the resulting moment becomes zero. Also, the taper plays an important role, because the pointed wing with same landing flap span has more wing area influenced by the landing flap, than the rectangle wing (at the same time less surface at the wing tip burdened with small lift coefficient). The polar, which are measured with the appropriate rudder deflections, are called equilibrium-polar . Later investigations resulted in that landing flaps at the delta wing root are already sufficient, in order to raise the lift over the whole span. The induction causes that ai drops more strongly towards the wing tips which therefore increases the effective AOA.
|
Fig. 8 Landing flap order of the HVb. These landing flaps had a full moment balance around the horizontal axis of the airplane. In 1943, the HVc was assigned to the Aerodynamic Laboratory Goettingen from the Research-Institute, in order to make takeoff and landing measurements and determine the max. lift, which is the base for performance comparisons with tail airplanes. |
However, since flap foils have a smaller max. AOA, landing flaps in mid-span can cause premature local separations and thus prevent the effectiveness of the flap system. Wind tunnel measurements before 1945, using such landing flaps, led to the wrong opinion that the delta wing was unsuitable for landing flaps. It should be pointed out that the delta wing with a small flap in the correct place (the wing root) increases the lift in such a way that it is suitable for almost all aircraft designs, with the flight characteristics not being compromised. A strong taper is therefore, as stated, advantages. In order to get a quality graph with max. landing lift to resistance in the high-speed flight (to be used as a yardstick), one can refer the max. landing lift to the air-surrounded surface (without flaps), since the resistance in the high-speed flight is mostly friction resistance. With the wing-only, the value 1.0 can be easily achieved. With the tail airplane, the fuselage and the empennage would have to be added as surface. However, all these comparisons have their drawbacks. In this case, the boundary layer is not included, which can have substantial differences in the drag coefficients at Reynold numbers between three and twelve million during a laminar flow. The sweep does not prevent the laminar effect, as was shown with gliders.
Notes to the theoretical basis of the interpretation of the H II
Was it in the delta, with inner elevators, mainly the local airfoil moment ,which at large airfoil length caused the control moment 
, an increased sweep had to take over now this function.
During the transfer of the elevators into the aileron at the wing tips, the local depths remained small with large taper, so that the second integral (because of t2) can be neglected. The first, however, contains x, the distance of the wing component (represented by the t/4
-point) to the CG. For it to become really effective, x, which is the sweep, must be large. The H II, therefore, was supposed to receive
a stronger sweep and larger taper. When the lift distribution considerably influences the altitude control, it is reasonable to assume that
the wash-out of the wing must change proportionally with the lift coefficient. For balance reasons, the centre of lift must correspond with
the CG. of each half-wing in longitudinal direction; in addition, the wash-out changes with the rudder deflection. For example, with cl =
0.5, the combined aileron-elevators in zero position and the wings have a rigid wash-out of 5 0. If the pilot wants to fly now with cl = 1.0, the elevator deflection 
must be as large as the basic wash-out, thus 5o. So the term Variable Wash-Out developed. In the
ideal case, without chord moments, one has to multiply the lift distribution only with one factor, in this example 2. The form and its CG
remain unchanged. A prerequisite for it is that the wing depth at the end in the rudder area is small (by taper or high aspect ratio), or that the value 
becomes zero, as for example with a rotation of the whole wing tip. For a later project, the H III, the aileron-elevator
would have to be divided into several flaps, which would have to operate with different deflection angles, in order to represent the
necessary wash-out form more exactly. Would one then transition to the half of the wing-depth, thus receive double the H III aspect
ratio (H IV), then the local chord moment would have only one fourth of the value of the H III because of the depth square, with which cm is connected. The altitude control, due to the wash-out change, would then be more proportionally to cl. In other words, the
disturbance by the local moments (caused by the flap deflection) will be less significant For the H II, with smaller aspect ratio, another solution would be a rotating wing tip. The wash-out would then get a step but with 
the chord moment of the flap deflection
would equal zero. These considerations presuppose a airfoil whose cma = 0, throughout the whole wing.
In combination with the first point (the lift hole at the head of the sweep) one could now bring the rudders into neutral position and measure the speed of the airplane, so that the cl can be calculated and check the compliance with the design lift coefficient.
In addition, one can go the other way, calculate out of the design lift coefficient the speed, then correct the CG position in such a way that the flown and the theoretical speed correspond with the neutral rudder position; this process was later called "balancing out by the neutral rudder position".
|
|
|
Fig. 9 The wing-tip of the H II. The wash-out step obtained by the deflected aileron is visible at Y = 0.95. |
During flight testing of the H I the question came up in 1934: which form of the lift distribution should the new construction, the H II,
receive? The aileron yaw moments had been the determining factor with the H I for the controllability. The bell lift distribution 
with the zero tangent in y = 1 had resulted in a defined descending flow over the whole span and
with that an induced AOA. From the turning point of the lift distribution to the outside the induced AOA changed it's sign, even so the lift remained positive. With the calculation of the induced resistance distribution cl*t*ai in wing span direction the wing ends received
propulsion. With Y = 0.7 changed ai it's sign, that was something new; one could use negative induced resistance for the compensation
of aileron yaw. If the aileron would be enough from Y = 0.7 to 1, then the induced yaw moments would have the opposite sign. Thus
the correction of the aileron deflection would be reduced or even unnecessary by a full rudder deflection, the rudder could then become
much smaller. Since the lift distribution form doesn't change much by variable wash-out during the elevator deflection, then this effect is
attainable with all lift coefficients thus all speeds. Aileron and rudders will then be separate and independent, as long as the bell
distribution (the turning point) was achieved. That was the theory of the lift distribution for the H II.
The washout step at the transition from ailerons to the fixed, immovable wing tip (called ear) at Y = 0.95 had a good affect on the yaw in the H I and it should therefore remain. Besides, the aileron-elevator, which reaches from Y = 0.7 to 0.95, appeared as quite small. It was designated therefore from half the span and up (Y = 0.5 to Y = 0.95). It also resulted that wing washout needed for the bell distribution became smaller with larger taper of the wing compared with a small taper or with the rectangle wing. Thus a large taper was not only advantages for the wing volume, but also for the necessary washout. The calculation of the local cl load resulted, that with increased taper of troot / twing-tips = 8.6 it reached a maximum at Y = 0.37. That, however, is almost at the lift center, which is in the bell at Y = 0.33. A separation of the flow starting at Y=0.37 should therefore hardly resulted in a change in CG, at least it should be controllable. That means "Spin resistance" or at least controllability in the extreme flight. The disadvantage of the bell distribution, an about 33% higher induced resistance with same span compared to a wing with elliptical lift distribution,
|
The airfoil distribution over the wing span, however, is likewise determined by the bell distribution, as the airfoil at the wing tip can be symmetrical, because there cl is always small, and even a triangle wing has near Y = 1 a small cl. The separation of the flow is therefore there not to be feared.
Within the range from Y = 0.3 to 0.4 should the separation begin, even at a camber of the airfoil middle line within this area is this fulfilled. The max. camber can, at last, be at the wing root . It is obvious to shape the wing linear from the root airfoil to the wing tip airfoil and to use a fixed-pressure-point airfoil at the root(cmo = 0). With the formulas of Birnbaum for cao and cmo the center line of the root airfoil was drawn and modified point for point in such a way, until cm0 = 0 was achieved.
Attempt of a repetition: H XIV " Colonia "
Beside the building the H XV c and the HO 33 there was a third attempt to build Horton type in Germany after the Second World War: it was the H XIV which was almost ready for flight at the end of the war.
The motivating force in the Aerodynamic Association Kolon was E. Cilsik. The project was pursued in an extensive correspondence across the Atlantic away. Lack of funds led after five years, in 1965, for cancellation of the work. At this time the fuselage mockup was finished. Wind tunnel experiments with models, building of the devices and many detail investigations had preceded.
Originally the "Colonia" was supposed to get the airfoil of the H IV. That's how the H XIV was built toward end of the war. 1963 the airfoil was changed to one with a larger laminar extension, unfortunately in vain.
Special features of this design were the wing narrowing near the center piece, the small fins on the wing at 6.40 meters of the half span and the rear of the fuselage developed as the dive brake.
In January 1965 the project H XIV "Colonia" was given up, even though after thorough testing of the prototype in an improved version with 15 meters wing span could be counted on having a lift/drag ratio of 38 to 40. These where excellent performances for that time for a 15-Meter-Glider with rigid airfoil.